第13章 存储

Storage Access

操作系统按块拿取数据，但数据库以记录为单位

对于数据库系统，io开销会影响效率，需要找到io操作影响最小的方案

buffer 提供了内存与数据库系统之间的数据缓冲区

buffer manager 负责buffer中数据的调度

buffer manager

如果buffer中有需要的块，向系统返回块在内存中的地址

如果没有，需要在buffer中为块提供一个空间，如果没有就需要替换其他无用的块；然后从内存中读入需要的块，并返回块在内存中的地址

替换操作规则

LRU least recently used

同操作系统的lru，最近最多的数据很有可能之后很长时间不再用到

加强版的是使用完立即丢弃Toss-immediate

MRU Most recently used最频繁使用

还有强制写出forced output，以及钉住块Pinned block（读写时不能有另外的操作）

File Organization 文件组织

数据库记录存放的文件形式、结构由DBMS决定，并向操作系统申请空间

定长记录

按条存放，可能会跨块，分配固定空间

会造成空间浪费，需要定期清理碎片

清理碎片的方式有

  • 压缩空间
  • 把最后一条记录放到被删除的记录的位置上
  • 使用空闲块链表，定义记录头部为链表头

变长记录

如何让dbms得知记录的大小来分配空间

  • 使用end of record符号表示记录末尾
  • 删除和增长都很困难

分槽式页结构 Slotted Page Structure

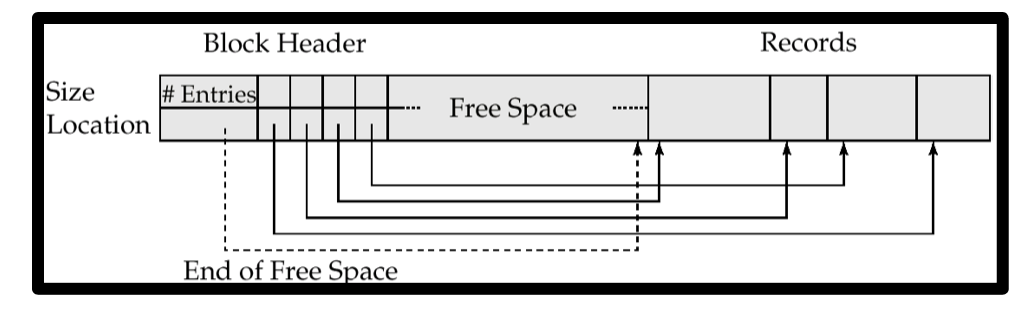
image-20231128140338148

页头包括

  • 记录的条数
  • 块中空闲空间的末尾地址
  • 每条记录的地址与大小

把空闲空间夹在中间，可以减少移动记录的开销

每条记录的结构如下

image-20231128140500007

其中，可以把变长属性的地址与大小属性放在最前面，后面是定长属性，然后是变长属性

空值的位图可以是0000

记录组织 Organization of Records

堆 heap

记录随机放，不受约束

记录经常不需要移动

为了随机放，需要维护一张空闲空间表，记录每块空闲空间的地址

image-20231128141549845

可以使用二级索引，比如上图对第一个列表每四块建立一个索引，为四块中的空闲空间最大值，便于寻找

顺序 Sequential

有序的记录摆放有利于查询，但维护开销大，需要大量时间进行排序

依据**搜索健（search key）**排序

使用指针链表控制删除和插入

插入时，如果有空闲位置就插入，没有就将记录插入到溢出块，更新链表

哈希 Hashing

B+树

聚集 Cluster

复合表的聚集就是对连接的表的结果直接存储存为聚集文件，这样不需要进行多次连接操作

但单表查询效率和维护开销会变得更大

基于列的存储

不讲了，但是对列的操作查询效率更高，便于压缩等等

第14章 索引

哈希索引不考

B+索引了解

剩下的要考

查询时要建什么索引，什么索引能提高效率？

概述

目的：提高查询效率

结构

  • search key 索引域 用于查询的属性或属性集合
  • pointer 指向数据文件中的记录的指针

有序索引 ordered indices

要考虑的因素

  • 访问方式
  • 访问时间
  • 插入时间
  • 删除时间
  • 占用空间

主索引 Primary index

也叫做聚集索引 clustering index

一般建立在主键上，但不一定建立在主键上

索引文件建立在有序域的数据文件的search key上的就是主索引

只有一个

辅助索引 secondary index

索引文件建立在无序域的数据文件的就是辅助索引，当然有序的数据文件也可以建立辅助索引，只要索引不是建在search key上

也叫做非聚集索引 non-clustering index

可以多个

一定是稠密索引（不然需要扫描那等于没建索引），且对于每条记录都有指针指向

下图的辅助索引建立在表的非排序域，属性工资上

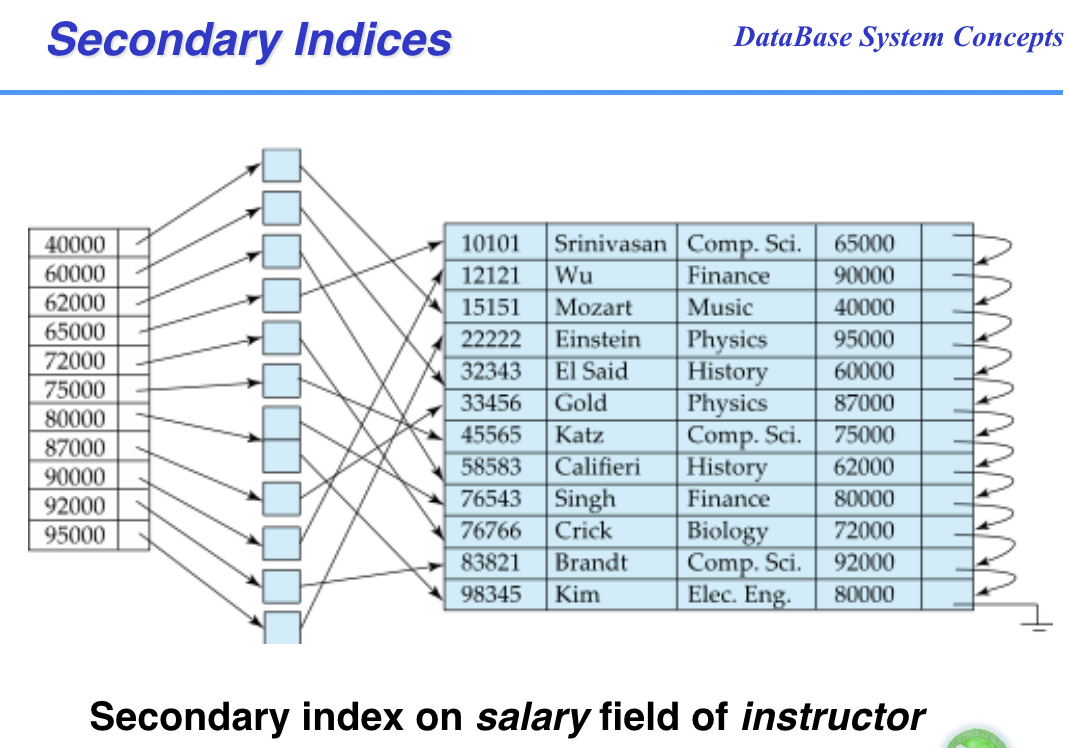
image-20231128151321941

稠密索引 Dense Indices

search key每个取值都有体现的索引就是稠密索引

查询效率高

稀疏索引 Sparse Indices

不是稠密索引的就是稀疏索引

可以按块建立稀疏索引，因为io操作也按块存取，方便使用

多级索引 Multilevel Index

如果索引本身也很大，那么有必要使用多级索引

可以使用B+树管理多级索引

索引的搜索

  • 首先，根据搜索健定位索引记录的第一条记录

  • 然后，顺序搜索直到找到需要的记录

  • 一般地，稀疏索引的搜索慢于聚集索引

  • 当一个文件被调整时，所有的在这个文件上的索引必须进行更新

  • 顺序搜索对主索引效率很高，但是对辅助索引效率较低

哈希索引 Hash Indices

就是用哈希表管理组织的索引，不考

索引相关SQL

1
create [unique|cluster|noncluster] index I on R(name,sex)
1
drop index I

索引的选择与效率优化

  • 主索引一般使用等于号判定，这样搜索效率提高
  • 辅助索引可以使用大于、小于、等于号
  • 同时，不指定主索引而单独指定辅助索引一般不利于搜索

结构图

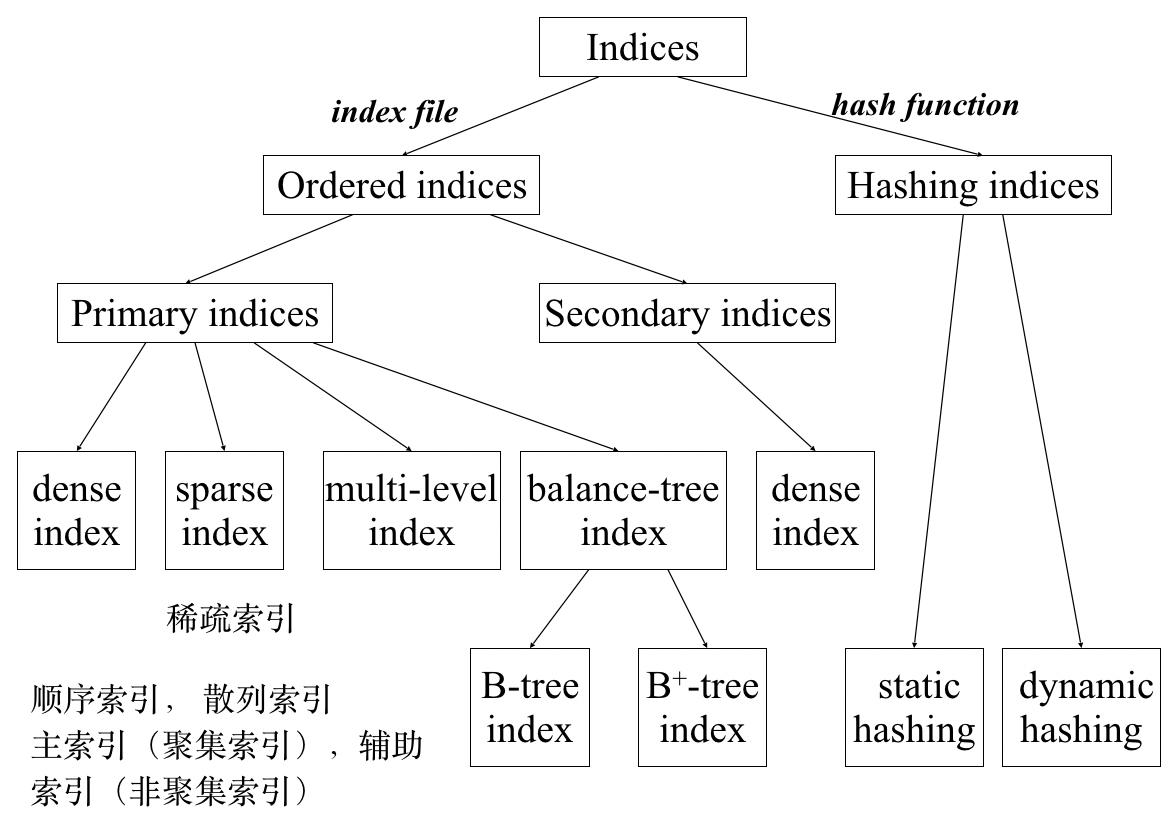
image-20231128152631729

第15章 查询处理

查询处理的基本步骤

  • 对语句进行语法分析和翻译

    翻译成关系代数

  • 进行查询优化

  • 执行

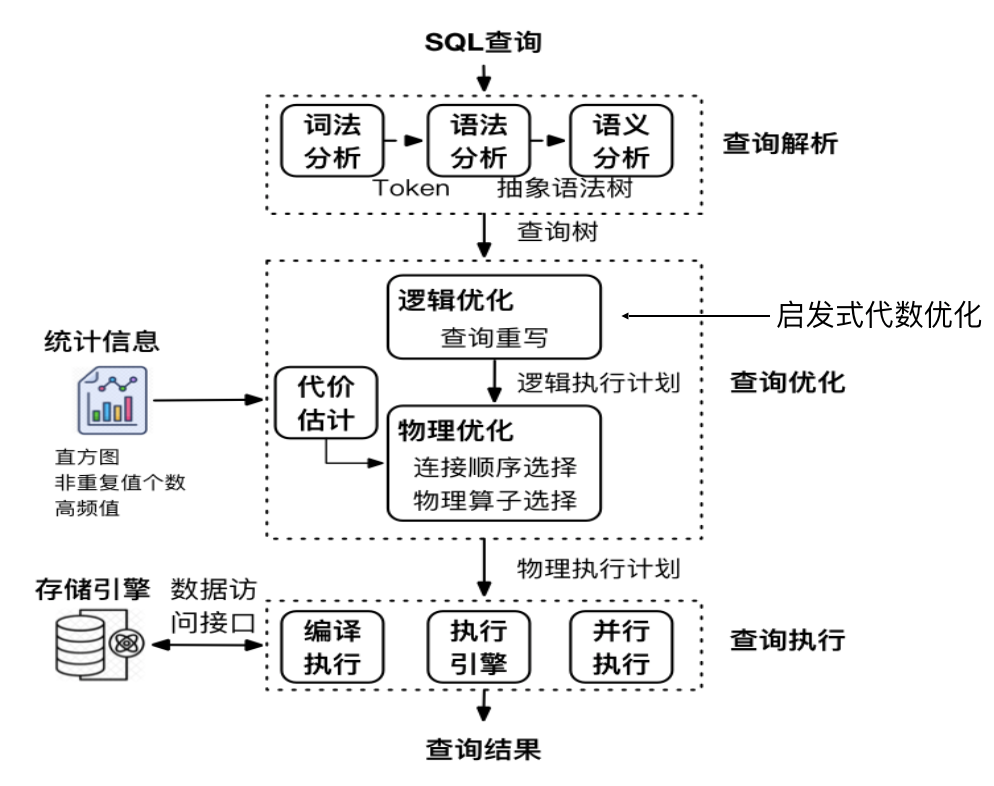
image-20231205131000213

查询代价估算

代价的衡量

  • 存储结构性能
  • IO性能（磁盘访问时间）（主要优化）
  • CPU
  • 网络

而在磁盘访问时间中，主要关注

  • 寻道时间
  • 读取时间
  • 写入时间

将读取和写入时间统一为传输时间，有以下关系

tT–传输时间tS–寻道时间对b块+S次寻道总时间b∗tT+S∗tSt_T – 传输时间 \\ t_S – 寻道时间 \\ 对b块+S次寻道总时间 \\ b * t_T + S * t_S

当然，这与buffer的大小也有关系，并且还有CPU的耗时，以及内部传输也需要考虑

文件扫描 File Scan

线性扫描

把整个表全部块都扫描一次（默认全部块连在一起，只寻道一次）

T=br∗tT+tST = b_r * t_T + t_S

如果查询条件是对候选键的，因为候选键唯一确定，故找到就结束，平均查找时间为

T=br/2∗tT+tST = b_r / 2 * t_T + t_S

二分查找

默认全部块连在一起，且有序排列

寻道需要重复执行以确定头、尾、中间

T=⌈log2(br)⌉∗(tT+tS)T = \lceil log_2(b_r) \rceil *(t_T + t_S)

如果条件是定义在排序域上的等值查询，结果一块放不下，传输时间会增加而寻道不会

索引查找

条件在索引域上查询

定义在候选键上的主索引等值查询

只会有一条结果

T=(hi+1)∗(tT+tS)hi表示索引树的深度，需要hi∗(tT+tS)查找索引然后用一次(tT+tS)看数据T = (h_i + 1) * (t_T + t_S) \\ h_i表示索引树的深度，需要h_i*(t_T + t_S)查找索引\\ 然后用一次(t_T + t_S)看数据

定义在非候选键上的主索引等值查询

结果有多条，主索引确保记录有序

T=hi∗(tT+tS)+tS+tT∗bhi表示索引树的深度，需要hi∗(tT+tS)查找索引tS表示有序只寻道一次b表示含有结果的块数T = h_i * (t_T + t_S) + t_S+t_T*b \\ h_i表示索引树的深度，需要h_i*(t_T + t_S)查找索引\\ t_S表示有序只寻道一次\\ b表示含有结果的块数

定义在查询键上的二级索引等值查询

如果查询键是候选键

结果只有一条

T=(hi+1)∗(tT+tS)hi表示索引树的深度，需要hi∗(tT+tS)查找索引然后用一次(tT+tS)看数据T = (h_i + 1) * (t_T + t_S) \\ h_i表示索引树的深度，需要h_i*(t_T + t_S)查找索引\\ 然后用一次(t_T + t_S)看数据

与主索引一样

如果查询键不是候选键

结果有多条，但二级索引不有序

最坏情况下,索引查到的n个匹配记录可能都分别在不同块中T=(hi+n)∗(tT+tS)hi表示索引树的深度最坏情况下,索引查到的n个匹配记录可能都分别在不同块中\\ T = (h_i + n) * (t_T + t_S) \\ h_i表示索引树的深度

范围查询

以主索引为例，若要查σA≥V(r)\sigma_{A\ge V}(r)

T=(hi)∗(tT+tS)+tS+b∗tThi表示索引树的深度b是大于V的记录所在块数T = (h_i) * (t_T + t_S) + t_S+ b * t_T \\ h_i表示索引树的深度\\ b是大于V的记录所在块数

对于小于的不需要索引，直接从头开始查询即可，因为有序

如果建立在辅助索引上

T=(hi+n)∗(tT+tS)hi表示索引树的深度最坏情况下，认为n条记录分别在不同块中，n是大于V的记录的条数T = (h_i + n) * (t_T + t_S) \\ h_i表示索引树的深度\\ 最坏情况下，认为n条记录分别在不同块中，n是大于V的记录的条数

对于小于的只需要访问叶子索引一个个比较

多个条件与查询

如果有一个条件可以通过索引查找，处理就基于单个条件索引判断，再根据具体情况判断

多条件多索引视为复合key

多个条件或查询

只能一个一个扫描找，但如果有一个条件要求扫描全文件，就直接扫描全文件

非条件查询

扫描，或索引操作

第16章 查询优化

优化方法

基于代价估算

根据语句生成关系表达式，计算代价选择最优解

启发式优化

根据若干规则优化

  • 选择操作先执行
  • 投影操作先执行
  • 选择连接操作结合执行

等价变化规则

image-20231205140702346

image-20231205141045295

image-20231205141817371

image-20231205141840476

最后的外围投影操作不会对效率有太多影响

image-20231205142613124

image-20231205142719783

启发式优化构造步骤

  • 构造查询树
  • 按优化规则、变化规则进行优化

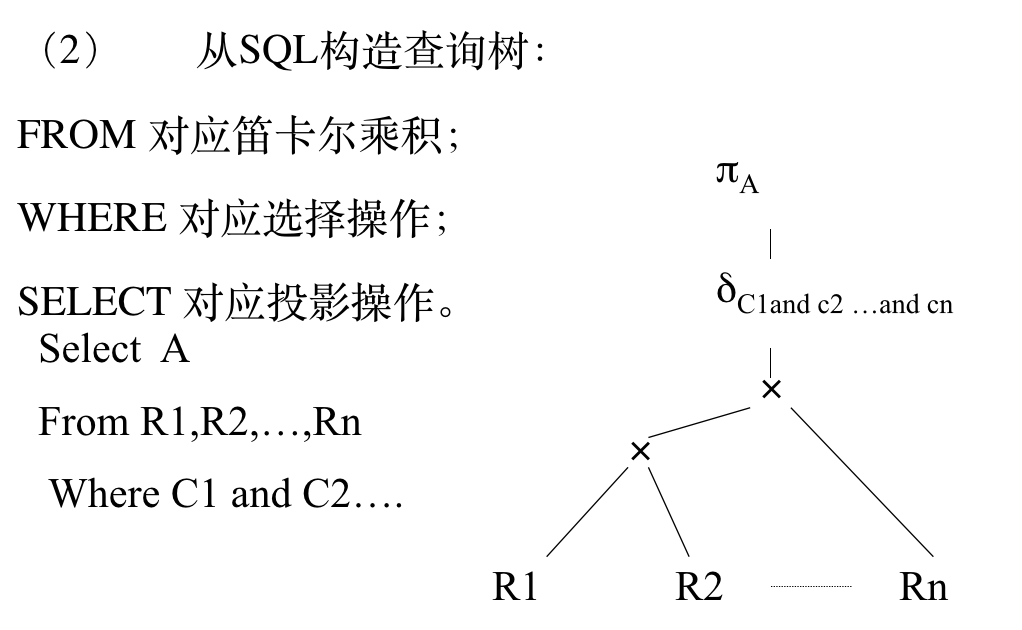
image-20231205143426511

  • 优化算法
    • 输入：一个关系代数表达式的语法树；
    • 输出：计算表达式的一个优化程序。
    • 执行步骤：对查询树从顶至下优化：
      1. 利用选择串接律，将选择操作分成单个独立；
      2. 对于每个选择操作，利用选择的交换律、和投影的交换律、和连接/笛卡尔乘积的分配律、和集合操作的分配律，使其尽可能移到靠近叶节点（为了让选择操作先执行）；
      3. 对于每个投影操作，利用投影串接律、和选择的交换律、和连接/笛卡尔乘积的分配律、和集合操作的分配律，使其尽可能移到靠近叶节点或删除某些投影操作（为了让投影操作先执行）；
      4. 使用选择、投影的串接律，选择、投影的交换律，将串接的多个选择和投影组合成一个（减少扫描次数）；
      5. 利用笛卡尔乘积/连接/集合操作的结合律，按照小关系先执行的原则，安排操作顺序；
      6. 组合笛卡尔乘积和相继的选择操作为连接操作；
      7. 对每个叶节点加必要的投影操作，消除对查询无用的属性；（如果之前投影做得好，此时不需要这个操作）
      8. 分组。每个二元运算（笛卡尔乘积、连接、集合操作）与其直接祖先（不越过别的二元运算节点）的一元运算节点（投影、选择），分为一组，如其子孙节点一直到叶节点皆为选择或投影，也并入该组。使每组的操作可由单个存取程序（一条生产线）完成。