第九章关系

9.1 关系及其性质

9.1.1 关系的概念

二元关系(binary relation) A，B为集合，一个从A到B的二元关系是A×B的子集
有序对(ordered pairs) 形如（a，b）的有序对，a来自A，b来自B
使用记号 $aRb表示(a,b)\in R$ ，称a与b有关系R

9.1.3 关系的性质

集合A上的关系是从A到A的关系，也就是A×A的子集（subset）

n元素集合上有 $2^{n^2}$ 个关系.原因是A有n个元素时，A×A有 $n^2$ 个元素，又n个元素的集合有 $2^n$ 个，故A×A有 $2^{n^2}$ 个子集，就是 $2^{n^2}$ 个关系

**自反性（reflexive）**

若对每个元素 $a\in A$ 有 $(a,a)\in R$ ，那么定义在集合A上的关系R称为自反的

**对称性（symmetric）与反对称性（antisymmetric）**

对于任意 $a, b\in A$ ，若只要 $(a, b)∈R$ 就有 $(b,a)∈R$ ,则称定义在集合A上的关系R为对称的。

对于任意 $a, b\in A$ ，若 $(a, b)\in R$ 且 $(b, a)\in R$ ,一定有a=b,则称定义在集合A上的关系R为反对称的。

**传递性（transitive）**

若对于任意 $a,b,c\in A$ , $(a, b)\in R$ 并且 $(b,c)∈R$ 则 $(a,c)\in R$ ,那么定义在集合A上的关系R称为传递的。

9.1.5 关系的组合

设R是从集合A到集合B的关系,S是从集合B到集合C的关系,R与S的合成是由有序对(a，c)的集合构成的关系，其中 $a∈A,c\in C$ ,并且存在一个 $b∈B$ 的元素，使得 $(a,b)\in R且(b,c)\in S$ 。我们用 $S\circ R$ 表示R与S的合成( the composite of R and S)

设R是集合A上的关系。R的n次幂 $R^n$ (n=1,2,3,…)递归地定义为

$R^1=R,\\R^{n+1}=R^n\circ R$

定理： 集合A上的关系R是传递的，当且仅当对n=1，2，3，…有
$R^n\subseteq R$

9.2 n元关系及其应用

设 $A_1,A_2,...,A_n$ 是集合,定义在这些集合上的n元关系是 $A_1×A_2×...×A_n$ 的子集。这些集合 $A_1,A_2,...,A_n$ 称为关系的域(domains),n称为关系的阶(degree)

9.2.3 数据库和关系

当n元组的某个域的值能够确定这个n元组时，n元关系的这个域就叫作主键（primary key）。这就是说，当关系中没有两个n元组在这个域有相同的值时，这个域就是主键。
常常要从数据库中增加或删除记录。由于这一点，一个域是主键的性质是随时间而改变的。所以，应该选择那种无论数据库怎样改变都能继续存在的域作为主键。

一个关系当前含有的所有n元组称为该关系的外延（extension）。数据库更持久的内容，包括它的名字和属性，则称为数据库的内涵（intension）。

选择主键的时候，应当选择那种能够为本数据库所有可能的外延充当主键的域。要做到这一点，就必须认真考察数据库的内涵，以便理解可能在外延中出现的n元组集。

在一个n元关系中，域的组合也可以唯一地标识n元组。当一组域的值确定一个关系中的n元组时，这些域的笛卡儿积就叫作复合主键（composite key）。

9.2.4 n元关系的运算

投影（projection）

最功利的理解：

$P_{a_1,a_2,...,a_m}$ 表示保留第ai列，同时要整合相同项

换句话说，投影P删除了n元组的n一m个分量，保留了第 $a_1,a_2,...,a_m$ 个分量。

连接（join）

最功利的理解：

合并表格同类项

换句话说，连接运算符 $J_p$ 将m元组的后p个分量与n元组的前p个分量相同的第一个关系中的所有m元组和第二个关系的所有n元组组合起来产生了一个新的关系。

9.3 关系的表示

9.3.2 矩阵表示

特别地，对矩阵的合成，有

$M_{S\circ R}=M_R\oplus M_S$

还可以推出

$M_{R^n}=M_R^{[n]}$

9.3.3 用图表示关系

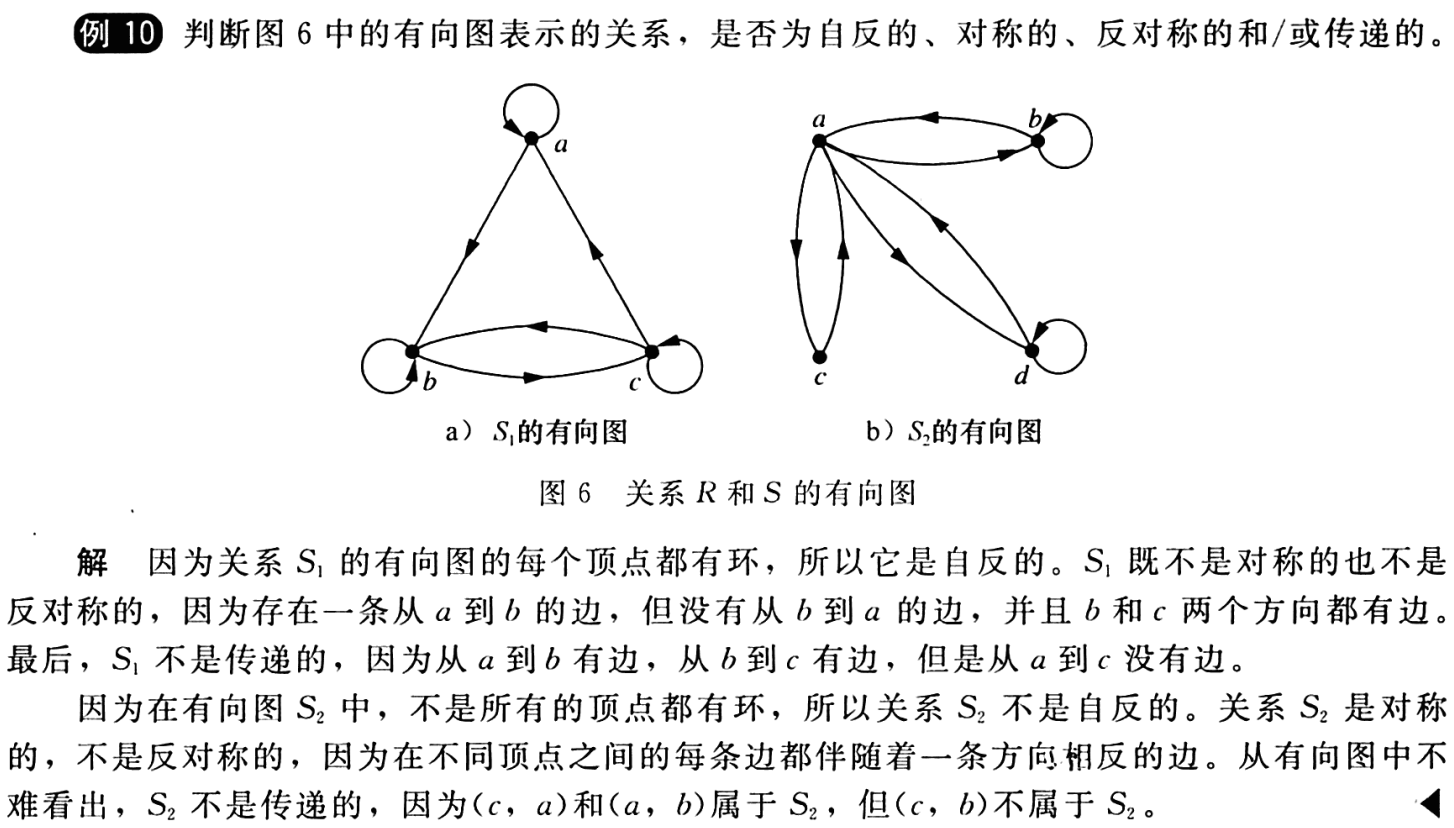
表示关系的有向图可以用来确定关系是否具有各种性质。

一个关系是自反的，当且仅当有向图的每个顶点都有环。

一个关系是对称的，当且仅当对有向图不同顶点之间的每一条边都存在一条方向相反的边，因此，只要(x，y)在关系中就有(y，x)在关系中。

类似地，一个关系是反对称的，当且仅当在两个不同的顶点之间不存在两条方向相反的边。

最后，一个关系是传递的，当且仅当只要存在一条从顶点a到顶点b的边和1条从顶点b到顶点c的边，就有一条从顶点a到顶点c的边(完成一个三角形,其中每条边都是具有正确方向的有向边)。

9.4 关系的闭包（Closures of Relations）

若R是集合A上的关系，它可能具有或者不具有某些性质P，例如自反性、对称性或传递性。当R不具有性质Р时，我们将求在集合A上，包含关系R且具有性质Р的最小关系S。

设R是集合A上的关系，若存在关系R的具有性质P的闭包,则此闭包是集合A上包含R的具有性质P的关系S，并且S是每一个包含R的具有性质P的 $A×A$ 的子集。

简单理解就是，现在有一个集合A，不能满足一个指定的关系R，需要再添加若干有序对，使这个集合A满足关系R，我们容易知道这个集合A也满足大关系S，那么这个新的集合内的关系S就是闭包

自反闭包

关系R的自反闭包等于 $R\cup \Delta,\Delta=\{(a,a)|a\in A\}$ 是A上的对角关系

整数集上的关系 $R=\{(a,b)|a<b\}$ 的自反闭包是什么?

答： R的自反闭包是

$R\cup \Delta=\{(a,b)|a< b\}\cup\{(a,a)|a\in Z\}\\=\{(a,b)|a\le b\}$
对称闭包

关系R的对称闭包可以通过求关系与它的逆的并来构造，即 $R\cup R^{-1}$ 是关系R的对称闭包，其中 $R^{-1}=\{(b,a)|(a,b)∈R\}$

正整数集合上的关系 $R=\{(a,b)|a>b\}$ 的对称闭包是什么?

答： R的对称闭包是关系
$R\cup R^{-1} = \{(a,b)|a >b\}\cup \{(b,a)|a >b\}= \{(a,b) | a≠b\}$
传递闭包

靠人自己算出来,或者用有向图

9.4.3 有向图中的路径

定理： 设R是集合A上的关系。从a到b存在一条长为n(n为正整数)的路径,当且仅当 $(a,b)\in R^n$

9.4.4 传递闭包

求一个关系的传递闭包，等价于在对应的有向图内确定哪些顶点对之间存在路径

设R是集合A上的关系。连通性关系 $R^*$ 由形如(a,b)的有序对构成,使得在关系R中,从顶点a到b之间存在一条长度至少为1的路径。
因为 $R^*$ 由有序对(a，b)构成，使得存在一条从顶点a到b的长为n的路径，所以 $R^*$ 是所有 $R^n$ 的并集。

我们可以这样概括：

R —— 集合A上的关系，比如a认识b就有 $(a,b)\in R$

$R^n$ —— 迭代n次关系R后存在的关系。比如存在 $m_1,m_2,...,m_{n-1}\in R$ ,使得a认识 $m_1$ ， $m_1$ 认识 $m_2$ ，…, $m_{n-1}$ 认识b，那么 $(a,b)\in R^n$

$R^*$ —— 是所有存在的 $R^n$ 的并集，也就是说，只要存在a认识b的关系（这层关系链长度至少为1），那么 $(a,b)\in R^*$

定理： 关系R的传递闭包等于连通性关系 $R^*$

既然我们知道传递闭包等于连通性关系，我们考虑这个关系的计算问题。在一个有限的有向图中，确定两个顶点之间是否存在一条路径，不需要检测任意长的路径。正如下面的引理所示，检测不超过n条边的路径就足够了，这里n是集合中的元素个数。

引理: 设A是含有n个元素的集合，R是集合A上的关系。如果R中存在一条从α到b的长度至少为1的路径,那么这两点间存在一条长度不超过n的路径。此外,当a≠b时，如果在R中存在一条从a到b的长度至少为1的路径，那么这两点间存在一条长度不超过n-1的路径。

我们通过上面的分析，可以知道

$R^*=R\cup R^2\cup R^3 \cup...\cup R^n$

又由前面用矩阵表示关系的内容可得，表示关系的并集的0-1矩阵是表示这些关系的0-1矩阵的并，所以表示传递闭包的0-1矩阵是R的前n次幂的0-1矩阵的并。

定理： 设 $M_R$ 是定义在n个元素集合上的关系R的0-1矩阵。那么传递闭包 $R^*$ 的0-1矩阵是

$M_{R^*}=M_R \lor M_R^{[2]} \lor M_R^{[3]} \lor ...\lor M_R^{[n]}$

算法1:计算传递闭包的过程(时间复杂度O(n^4)) 
procedure transitive closure(Martix MR)//(MR是n×n的0-1矩阵)
A:= MR
B:= A
for i := 2 to n
A:= A⊕MR
R:= B∨A
return B//{B是表示R*的0-1矩阵}

9.4.5 沃舍尔算法（Warshall’s Algorithm）

算法1求出定义在n元素集合上的关系的传递闭包需要使用 $2n^3(n一1)$ 次比特运算。而沃舍尔算法只需要使用 $2n^3$ 次比特运算就可以求出这个传递闭包。

沃舍尔算法的基础是构造一系列的0-1矩阵。这些矩阵是 $W_0,W_1, …,W_n$ ,其中 $W_0= M_R$ 是这个关系的0-1矩阵，且 $W_k=[w_{ij}^{(k)}]$ 。

如果存在一条从 $v_i$ 到 $v_j$ 的路径使得这条路径的所有内部顶点都在集合 $\{v_1,v_2,…,v_k\}$ (表中的前k个顶点)中，那么 $[w_{ij}^{(k)}]$ =1，否则为0 (这条路径的起点和终点可能在表中的前k个顶点的集合之外)。

注意 $W_n=M_{R^*}$ ，因为 $M_{R^*}$ 的第 $(i,j)$ 项是1，当且仅当存在一条从 $v_i$ 到 $v_j$ 的路径，且全部内部顶点都在集合 $\{v_1,v_2,…,v_n\}$ 中(但这些就是有向图中的所有顶点)。

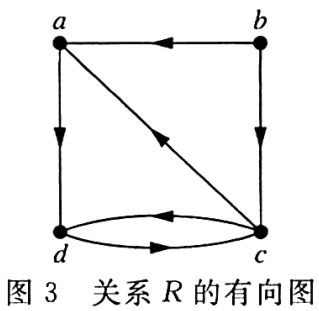
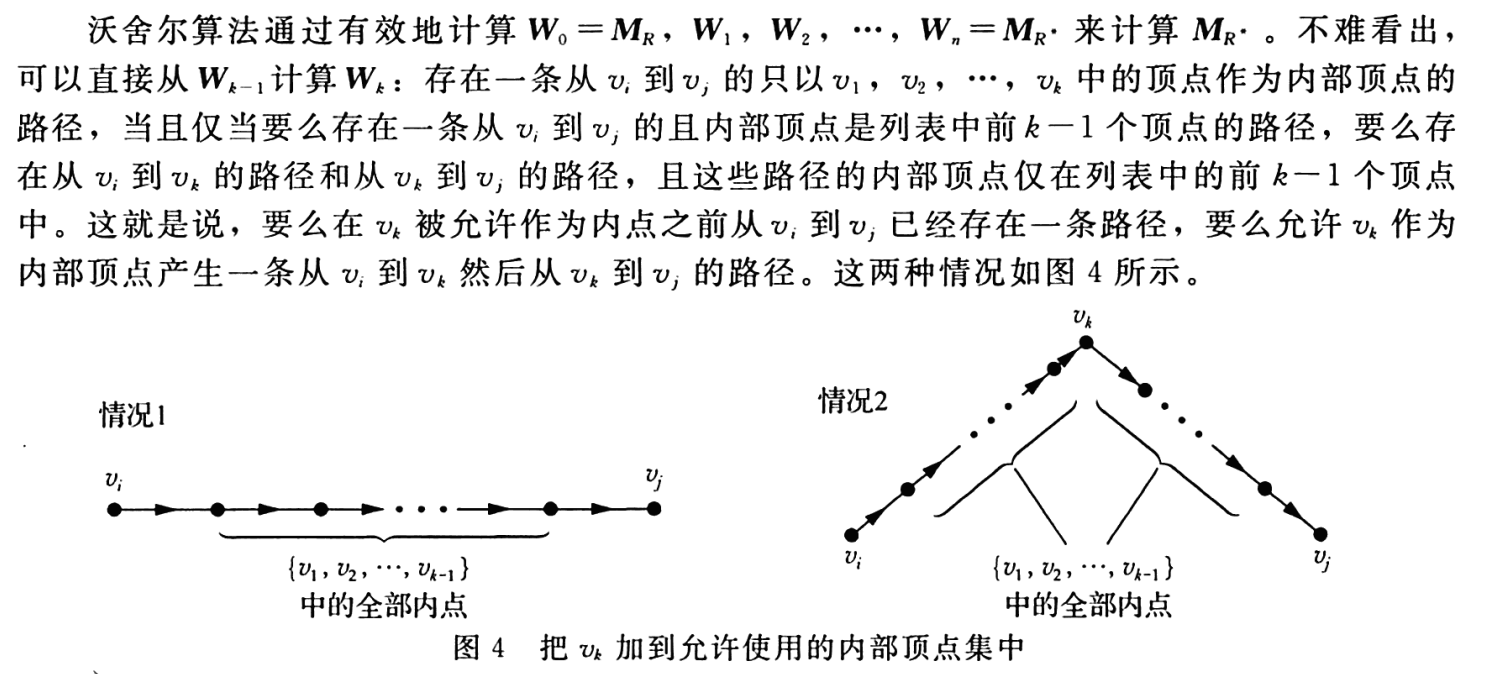
第一种类型的路径存在当且仅当 $w_{ij}^{[k-1]}=1$ ，第二种类型的路径存在当且仅当 $w_{ik}^{[k-1]}=1$ 和 $w_{kj}^{[k-1]}=1$ 。

于是， $w_{ij}^{[k]}=1$ 当且仅当 $w_{ij}^{[k-1]}=1$

或

$w_{ik}^{[k-1]}=1$ 和 $w_{kj}^{[k-1]}=1$

通俗点讲，现在路径有k-1个节点，要接上第k个节点

第一种方法是在队尾添加，要求第k-1个节点可通

第二种方法是在队中间添加，要求前面与后面的路径节点要可通

算法2	沃舍尔算法
procedure Warshall(Martix MR)// MR : n×n的0-1矩阵

W:=MR

for k:=	1 to n
	for i := 1 to n
		for j:= 1 to n
		Wij:= Wij∨(Wik∧Wkj)
		
return W		//{W=[Wij]是MR*}

9.5 等价关系（Equivalence Relations）

9.5.2 等价关系的概念

定义在集合A上的关系叫作等价关系，如果它是自反的、对称的和传递的。

通常记作a~b

每个元素都应该等价于它自身（自反性）
a和b是相互关联（a and b is related）的（对称性）

表示a是关联于b的，表达为“a is related to b”
若a_b，bc，则a~c（传递性）

下面介绍等价关系成立的一些例子(其实就一个)

模m同余关系

m是大于1的整数，

$R=\{(a,b)|a\equiv b(mod\ m)\}\\ a\equiv b(mod\ m)，当且仅当a-b能被m整除$

下面介绍等价关系不成立的一些例子

整除关系

定义在正整数关系上的整除关系a|b不是等价关系，因为2|4但没有4|2

9.5.3 等价类（Equivalence Classes）

设R是定义在集合A上的等价关系。与A中的一个元素a有关系的所有元素的集合叫作α的等价类。A的关于R的等价类记作 $[a]_R$ .当只考虑一个关系时，我们将省去下标R并把这个等价类写作[a]。

换句话说，如果R是定义在集合A上的等价关系，则元素a的等价类是 $[a]_R =\{s | (a,s)∈R\}$
如果 $b\in[a]_R$ ，b叫作这个等价类的代表元(representative)。一个等价类的任何元素都可以作为这个类的代表元。也就是说，选择特定元素作为一个类的代表元没有特殊要求。

9.5.4 等价类与划分（Partitions）

等价类构成A的划分，因为它们将A分成不相交的子集。

更确切地说，集合S的划分是S的不相交的非空子集构成的集合，且它们的并集就是S。

换句话说，一族子集 $A_i,i\in I\ (I是下标的集合)$ 构成了集合S的划分，当且仅当

$A_i\neq \oslash ，i \in I\\ A_i\cap A_j=\oslash,i\neq j\\ 和\\ \cup_{i \in I}A_i=S$

定理： 设 $R$ 是定义在集合 $S$ 上的等价关系，那么 $R$ 的等价类构成 $S$ 的划分。反过来，给定集合 $S$ 的划分 $\{A_i|i \in I\}$ ,则存在一个等价关系 $R$ ,他以集合 $A_i(i \in I)$ 作为他的等价类。

9.6 偏序（Partial Orderings）

9.6.1 偏序的概念与良序归纳原理

定义在集合 $S$ 上的关系 $R$ ，如果他是自反的，反对称的和传递的，就称为偏序。

集合 $S$ 与定义在其上的偏序 $R$ 一起称为偏序集（partially ordered set / poset），记作 $(S,R)$ 。集合中的成员称为偏序集的元素。

通常，我们采用记号 $\preceq$ 来表示任意一个偏序集中的序关系。例如，对偏序集 $(S,R)$ , $a\preceq b$ 表示 $(a,b)\in R$ .

使用这个符号是由于“小于或等于”关系是偏序关系的一个代表范例。

要注意的是，当a，b是偏序集 $(S,\preceq)$ 的元素时，不一定有 $a\preceq b$ 和 $b\preceq a$

比如在 $(Z^+,|)$ 中，2和3没有关系，3和2也没有关系。因为2$\nmid $3,3$ \nmid$2.

定义： 偏序集 $(S,\preceq)$ 中存在元素a和b,如果$a\preceq b $或$ b\preceq a$,则称a与b是可比的(comparable),

当a和b是S中的元素并且既没有 $a\preceq b$ ，也没有 $b\preceq a$ ，则称a与b是不可比的(incomparable)

吐槽一下这机翻翻译

偏序集 $(S,\preceq)$ 中的元素a和b称为可比的,如果$a\preceq b $或$ b\preceq a$

无话可说了，按这翻译来学，能学成什么样…

定义：

如果 $(S,\preceq)$ 是偏序集，且S中的每队元素都是可比的，则S称为全序集（totally ordered）或线序集(linearly ordered set)，且 $\preceq$ 称为全序或线序。

一个全序集也称为链(chain)。

对于偏序集 $(S,\preceq)$ ，如果 $\preceq$ 是全序，并且S的每个非空子集都有一个最小元素，就称他为良序集（well-ordered set）

定理：良序归纳原理（THE PRINCIPLE OF WELL-ORDERED INDUCTION）

设S是一个良序集。

(归纳步骤)

如果对所有 $y \in S$ ,

如果P(x)对所有 $x\in S$ 且 $x\prec y$ 为真,

则P(y)为真,

那么P(x)对所有的 $x\in S$ 为真。

9.6.2 **字典序（ Lexicographic Order）**

就正常理解的字典序，没什么好说的

**9.6.3 哈塞图（Hasse Diagrams）**

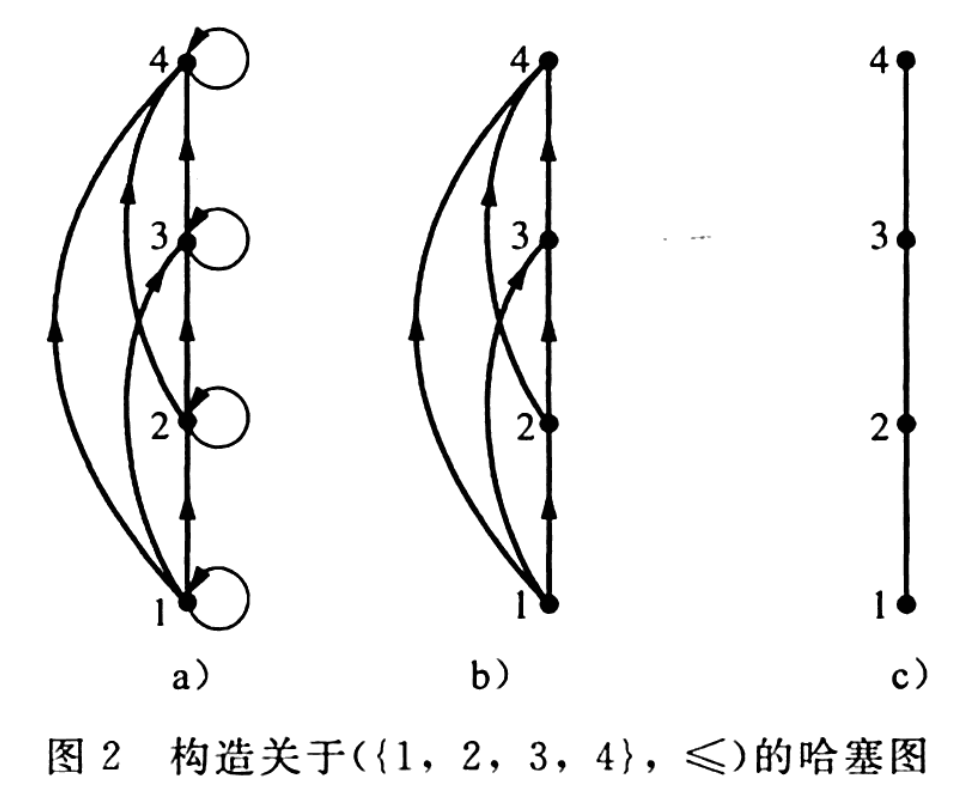
构造哈塞图的一般步骤：

一般说来，我们可以使用下面的过程表示一个有穷的偏序集 $(S,\preceq)$ 。

从这个关系的有向图开始。
由于偏序是自反的，所以在每个顶点a都有一个环(a，a),移走这些自反环。
下一步，移走所有由于传递性必须出现的边，因为存在一些其他的边而且偏序是传递的。也就是说，对于元素 $z\in S$ 如果 $r\prec z$ 且 $z\prec y$ ，则移走所有这样的边(r，y)。
最后，排列每条边使得它的起点在终点的下面。移走有向边上所有的箭头，因为所有的边“向上”指向它们的终点。

当所有的步骤执行以后，就得到一个包含足够的表示偏序信息的图,这个图称为 $(S,\preceq)$ 的哈塞图。

在偏序集 $(S,\preceq)$ 中，若 $x\prec y$ 且不存在元素 $z\in S$ 使得 $x\prec z\prec y$ ，则称元素 $y\in S$ 覆盖元素 $x\in S$ 。y覆盖x的有序对(x，y)的集合称为 $(S,\preceq)$ 的覆盖关系(covering relation)。

从对偏序集的哈塞图的描述中，我们可以看出，在 $(S,\preceq)$ 的哈塞图中的边是指向上面的边,并且与 $(S,\preceq)$ 的覆盖关系中的有序对相对应。

而且，我们可以从偏序集的覆盖关系中得到这个偏序集,因为它是它的覆盖关系的传递闭包的自反闭包。

9.6.4 极大元（Maximal）与极小元（Minimal）

偏序集中的一个元素称为极大元（Maximal），当它不小于这个偏序集的任何其他元素。即当不存在 $b\in S$ 使得 $a\prec b$ ，a在偏序集 $(S,\preceq)$ 中是极大元。

类似地，偏序集的一个元素称为极小元（Minimal），如果它不大于这个偏序集的任何其他元素。即如果不存在 $b\in S$ 使得 $b\prec a$ ，则α在偏序集 $(S,\preceq)$ 中是极小元。

使用哈塞图很容易识别极大元与极小元。它们是图中的“顶”元素与“底”元素,同时，一个哈塞图可以同时存在多个极大元与极小元。

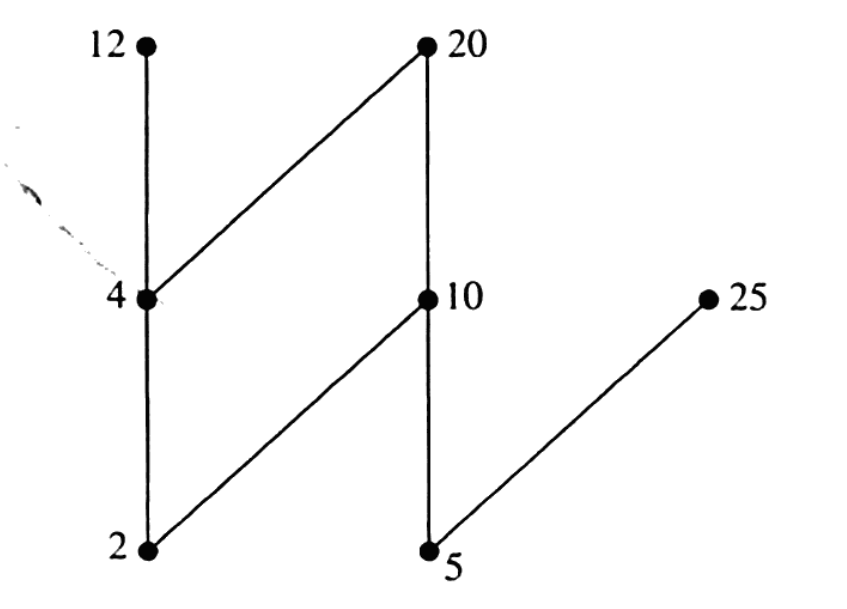
像上面这张图中，偏序集的极大元是12，20，25；偏序集的极小元是2，5。

有时在偏序集中存在一个元素大于每个其他的元素，这样的元素称为最大元（greatest element），即如果对所有的 $b\in S$ 有 $b\preceq a$ ，那么a是偏序集 $(S,\preceq)$ 的最大元。当最大元存在时，它是唯一的。

类似地，当一个元素小于偏序集的所有其他元素时，它称为最小元（least element），即如果对所有的 $b\in S$ 有 $a\preceq b$ ，那么a是偏序集 $(S,\preceq)$ 的最小元。当最小元存在时，它也是唯一的。

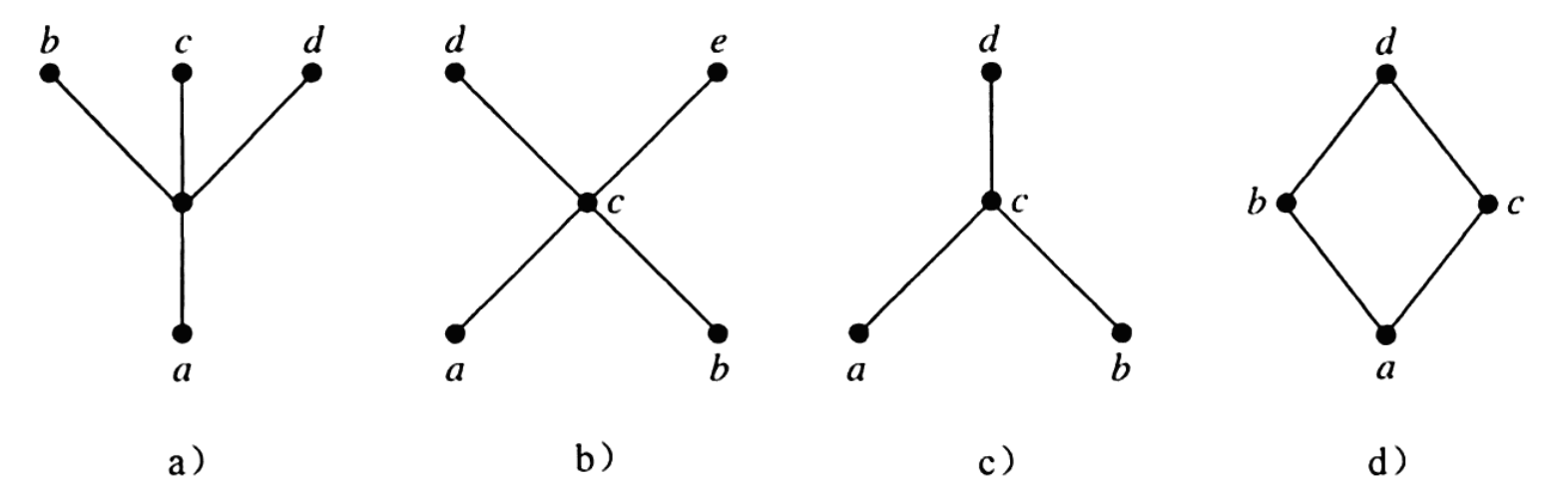
(a)的最小元是a，没有最大元
(b)没有最小元也没有最大元
©没有最小元，最大元是d
(d)的最小元是a，最大元是d

有时候可以找到一个元素大于或等于偏序集 $(S,\preceq)$ 的子集A中的所有元素。如果u是S中的元素，使得对所有的元素 $a\in A$ ，有 $a\preceq u$ ，那么u称为A的一个上界(upper bound)。

类似地，也可能存在一个元素小于或等于偏序集 $(S,\preceq)$ 的子集A中的所有元素。如果l是S中的一个元素，使得对所有的元素 $a\in A$ 有 $l\preceq a$ ，那么l称为A的一个下界(lower bound)。

如果元素a是一个上界并且它小于A的任何其他的上界,那么a叫作子集A的最小上界（least upper bound），记作 $lub(A)$ 。

即若任意 $a\in A$ 有 $a\preceq x$ ，并且对于A的任意上界z，有 $x\preceq z$ ，则x就是A的最小上界。

类似地，如果元素a是一个下界并且它大于A的任何其他的下界,那么a叫作子集A的最大下界（greatest lower bound），记作 $glb(A)$ 。

即若任意 $a\in A$ 有 $x\preceq a$ ，并且对于A的任意下界y，有 $y\preceq x$ ，则x就是A的最大下界。

最小上界和最大下界若存在，都是唯一的

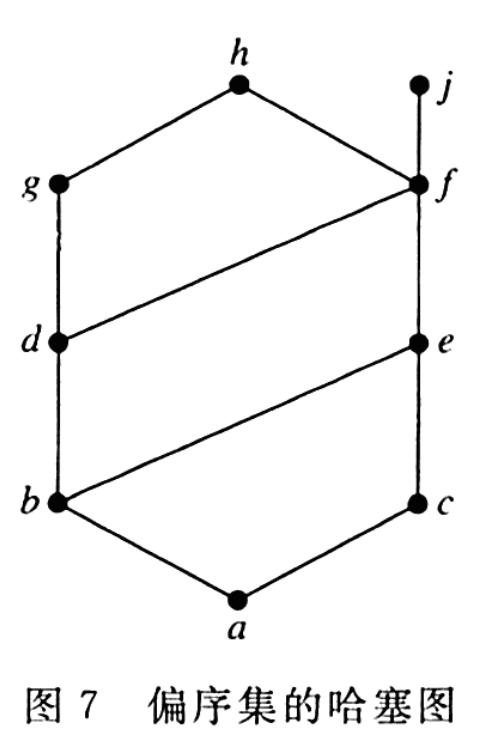
对图中的偏序集

子集{a,b,c}的上界为e f j h,下界为a,最小上界为e,最大下界为a
子集{j,h}没有上界，下界为a b c d e f，没有最小上界，最大下界为f
子集{a,c,d,f}的上界为f h j,下界为a,最小上界为f,最大下界为a

9.6.5 **格（ Lattice）**

如果一个偏序集的每对元素都有最小上界和最大下界，就称这个偏序集为格。

**9.6.6 拓扑排序（Topological Sorting）**

我们从定义开始。如果只要aRb就有 $a\preceq b$ 则称一个全序 $\preceq$ 与偏序R是相容的(compatible)。从一个偏序构造一个相容的全序称为拓扑排序.

引理： 每个有穷非空偏序集 $(S,\preceq)$ 至少有一个极小元。

找出与偏序集 $(\{1，2，4，5，12，20\}，|)$ 相容的一个全序。

第一步是选择一个极小元。这个元素一定是1，因为它是唯一的极小元。
下一步选择 $(\{2，4，5，12，20\}，|)$ 的一个极小元。在这个偏序集中有两个极小元，即2和5。我们选择5。
剩下的元素是 $\{2，4，12，20\}$ 。在这一步，唯一的极小元是2。下一步选择4，因为它是 $( \{4，12，20\}，|)$ 的唯一极小元。
因为12和20都是 $(\{12，20\}，|)$ 的极小元，下一步选哪一个都可以。我们选20，只剩下12作为最后的元素。
这产生了全序

$1\prec 5\prec 2\prec 4\prec 20\prec 12\\$

写完,洗澡,舒服